Un préstamo es un contrato por el que una de las partes, denominada prestamista, entrega dinero a otra llamada prestatario. Este por su parte, se compromete a devolver al prestamista el dinero prestado más los intereses, fijando para ello unas condiciones y un plazo de tiempo determinado.
Muchas son las alternativas a este acuerdo entre las partes. Desde la flexibilidad absoluta, dejando en manos del prestatario la devolución de los capitales, a establecer un cuadro en el cual se especifique exactamente qué importes y en qué fechas deben ser satisfechos.
La amortización de un préstamo es el proceso que sigue el prestatario para ir devolviendo el dinero inicial, más los intereses, al prestamista. Más allá de acuerdos puntuales, existen diversos métodos que la práctica financiera ha ido estableciendo con el tiempo, y que pueden ser utilizados por las partes en un proceso de negociación que incluya la forma en que se reembolsa el capital.
Caso paradigmático en nuestro en nuestro entorno es el denominado método francés de cuotas constantes, de gran popularidad por ser el habitualmente utilizado en los préstamos inmobiliarios por las entidades financieras.
Alternativamente al método de cuotas constantes, que en principio suponen el mismo esfuerzo por parte del prestatario durante toda la vida de la operación, existen métodos cuyas cuotas son variables. Estos son diversos, y suponen un incremento o una disminución de los pagos periódicos a realizar para la devolución del capital. Veamos algunos y su característica, recordando en primer lugar las de método francés.
El método francés se caracteriza por el hecho de que todas las cuotas periódicas son constantes durante todo el plazo de la operación. Ello supone que el tipo de interés aplicado es ser el mismo para todo el período (lo que no impide que se pueda revisar según se pacte entre las partes)
La expresión analítica de la cuota a pagar es:
Muchas son las alternativas a este acuerdo entre las partes. Desde la flexibilidad absoluta, dejando en manos del prestatario la devolución de los capitales, a establecer un cuadro en el cual se especifique exactamente qué importes y en qué fechas deben ser satisfechos.
La amortización de un préstamo es el proceso que sigue el prestatario para ir devolviendo el dinero inicial, más los intereses, al prestamista. Más allá de acuerdos puntuales, existen diversos métodos que la práctica financiera ha ido estableciendo con el tiempo, y que pueden ser utilizados por las partes en un proceso de negociación que incluya la forma en que se reembolsa el capital.
Caso paradigmático en nuestro en nuestro entorno es el denominado método francés de cuotas constantes, de gran popularidad por ser el habitualmente utilizado en los préstamos inmobiliarios por las entidades financieras.
Alternativamente al método de cuotas constantes, que en principio suponen el mismo esfuerzo por parte del prestatario durante toda la vida de la operación, existen métodos cuyas cuotas son variables. Estos son diversos, y suponen un incremento o una disminución de los pagos periódicos a realizar para la devolución del capital. Veamos algunos y su característica, recordando en primer lugar las de método francés.
El método francés se caracteriza por el hecho de que todas las cuotas periódicas son constantes durante todo el plazo de la operación. Ello supone que el tipo de interés aplicado es ser el mismo para todo el período (lo que no impide que se pueda revisar según se pacte entre las partes)
La expresión analítica de la cuota a pagar es:
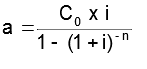
Siendo Co el capital inicial, i el tipo de interés, y n el número de períodos. Despejando la a, la expresión de la cuota a pagar es:
Supongamos un préstamo de 200.000 €, amortizable en 3 años con pagos trimestrales pos pagables, von el primer pago el 31 de marzo de 2022. Si el tipo nominal de interés anual es del 6%, el tipo trimestral es del 1,5%, y la cuota trimestral constante será:
Supongamos un préstamo de 200.000 €, amortizable en 3 años con pagos trimestrales pos pagables, von el primer pago el 31 de marzo de 2022. Si el tipo nominal de interés anual es del 6%, el tipo trimestral es del 1,5%, y la cuota trimestral constante será:
Los intereses devengados del primer período serán:
200.000 € x 0,015 = 3.000 €
La amortización del capital será la diferencia entre la cuota trimestral constante calculada y los intereses devengados en el período:
18.336,00 € – 3.000,00 € = 15.336,00 €
Para preparar el cuadro de amortización podemos utilizar una hoja Excel con la siguiente estructura:
Para el importe de la cuota total colocamos el importe calculado, así como la de los intereses, y obtendremos la cuota de amortización de capital por diferencia. El capital amortizado y el capital pendiente se obtienen inmediatamente.
Una de las alternativas a utilizar la fórmula que hemos señalado, es hacer uso de la función PAGO que se activa colocándonos en la casilla de la primera cuota y presionando fx en la barra superior.
Activada la función, en el cuadro que se despliega incluimos el tipo de interés (6%/4) el número de períodos (16) y el importe del valor actual del préstamo (-200.000) Aceptando nos aparece el resultado como vemos en el cuadro de la derecha.
Procedemos a cumplimentar los campos del resto de períodos, con la misma cuota a pagar y el cálculo de los intereses, obteniendo el cuadro de amortización:
Procedemos a cumplimentar los campos del resto de períodos, con la misma cuota a pagar y el cálculo de los intereses, obteniendo el cuadro de amortización:
Como podemos ver el capital pendiente al final del último período es cero, habiéndose reembolsado en su totalidad.
Hasta aquí la aplicación práctica del método francés de cuotas constantes.
Un primer método de amortización de cuotas variables, en este caso decrecientes, es el denominado método lineal. Este método se caracteriza por el hecho de que en todos los períodos se devuelve la misma cantidad de capital, a la cual se le añaden los intereses devengados en el período.
La cuota de amortización de capital se obtiene con la siguiente expresión:
Siendo, aK la parte de amortización de capital en cada cuota, C0 el principal del préstamo y n el número de períodos. En nuestro ejemplo:
Para el cuadro de amortización utilizamos el mismo esquema anterior, en el que introducimos en esta ocasión el capital a amortizar, los intereses del período calculados sobre el capital pendiente, y la cuota total como suma de ambos.
De la misma forma procedemos con el resto de períodos y obtenemos el cuadro de amortización, en el que apreciamos que de nuevo que en el periodo 12 se reembolsa todo el capital.
Como vemos la cuota es descendiente desde los 19.666,67 € iniciales hasta los 16.916,67 € de la última cuota. Si lo comparamos con el método de cuota constante que arrojaba una cuota igual para todos los períodos de 18.336,00 €, el método lineal supone un esfuerzo superior al inicio, que va descendiendo con el paso del tiempo.
Muy posiblemente, un consumidor estaría más interesado en un método de cuota variable que fuera creciente y que supusiera un menor esfuerzo al inicio. De esta manera, podría hacer frente a las cuotas posteriores con unos ingresos superiores en caso de incrementos futuros, y haría el esfuerzo menor al poder destinar parte de los ingresos al inicio a otras obligaciones.
Siguiendo con nuestro ejemplo, supongamos ahora que partiendo del método de cuotas constantes y manteniendo el resto de condiciones iguales, se pacta un incremento cada año de la cuota trimestral de 1.000 €. Es decir se sumarían 1.000 a la cuota total a pagar en cada trimestre. Diríamos que estamos ante cuotas ascendentes aritméticamente.
Para calcular la primera cuota la expresión que utilizamos es la siguiente:
Muy posiblemente, un consumidor estaría más interesado en un método de cuota variable que fuera creciente y que supusiera un menor esfuerzo al inicio. De esta manera, podría hacer frente a las cuotas posteriores con unos ingresos superiores en caso de incrementos futuros, y haría el esfuerzo menor al poder destinar parte de los ingresos al inicio a otras obligaciones.
Siguiendo con nuestro ejemplo, supongamos ahora que partiendo del método de cuotas constantes y manteniendo el resto de condiciones iguales, se pacta un incremento cada año de la cuota trimestral de 1.000 €. Es decir se sumarían 1.000 a la cuota total a pagar en cada trimestre. Diríamos que estamos ante cuotas ascendentes aritméticamente.
Para calcular la primera cuota la expresión que utilizamos es la siguiente:
Siendo a la primara cuota, C0 el importe del préstamo, j el tipo de interés nominal anual, m el número de términos de amortización en un año, d la razón de la progresión (que puede ser positiva o negativa) n la duración de la operación, e i el tipo de interés efectivo anual.
Recordemos que el tipo de interés efectivo anual (o TAE) se calcula partiendo del tipo de interés nominal y de la frecuencia de capitalización: i = (1 + N/f)f – 1.
En nuestro ejemplo el tipo efectivo anual es i = (1 + 0,06/4)4 – 1 = 0,06136
Calculamos la primera cuota de nuestro ejemplo:
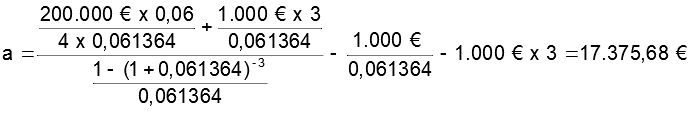
En nuestro ejemplo el tipo efectivo anual es i = (1 + 0,06/4)4 – 1 = 0,06136
Calculamos la primera cuota de nuestro ejemplo:
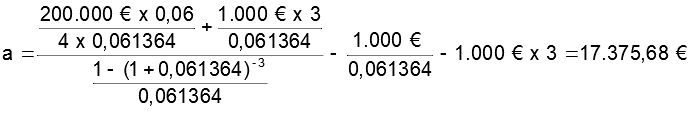
Para el importe de la cuota total colocamos el importe calculado, así como la de los intereses, siendo la cuota de amortización de capital la diferencia. El capital amortizado y el capital pendiente se obtienen por diferencia.
Procedemos para el resto de cuotas del año, e incrementamos la cuota en 1.000 € al inicio del segundo y del tercer año.
Otra posibilidad quizás más frecuente, es que en lugar de incrementar la cuota cada año, se incremente en cada período. En este caso, de nuevo la clave está den calcular la cuota inicial que sería:
Siendo a la primara cuota, C0 el importe del préstamo, j el tipo de interés nominal anual, m el número de términos de amortización en un año, d la razón de la progresión (puede ser positiva o negativa) n la duración de la operación, e i el tipo de interés efectivo anual.
Calculamos la primera cuota de nuestro ejemplo que en este caso se incrementará en 250 € trimestrales:
Calculamos la primera cuota de nuestro ejemplo que en este caso se incrementará en 250 € trimestrales:
Seguimos la mecánica habitual, incorporamos la cuota total en el cuadro de amortización, calculamos los intereses como siempre, y por diferencia obtenemos la amortización del capital.
Confeccionamos el resto del cuadro de amortización.
Otra posibilidad es que en lugar de incrementar la cuota total, lo que se incremente sea la cuota de amortización de capital. En este caso la expresión para obtener la primera cuota sería:
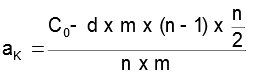
Siendo, aK la parte de amortización de capital de las primeras cuotas, C0 el principal del préstamo, del incremento anual de la cuota de amortización y n el número de períodos. En nuestro ejemplo si suponemos que la cuota se incrementa en 1.000 € cada año:
Para el cuadro de amortización utilizamos el mismo esquema de siempre, en el que introducimos el capital a amortizar, los intereses del período calculados sobre el capital pendiente, y la cuota total del período como suma de ambos.
Confeccionamos el resto del cuadro de amortización.
Como en los casos anteriores, el método permite que en el último período el capital quede totalmente reembolsado.
De nuevo, este último método podría adaptarse a incrementar la cuota cada período en lugar de hacerlo anualmente, como hemos mostrado en el ejemplo anterior.
Por otro lado, también es posible establecer un método de términos de amortización variables en progresión geométrica, cada año o cada período, sea respecto a la cuota o respecto a la amortización de capital. Para no extendernos en exceso, dejamos su desarrollo para otra ocasión.
Hasta aquí hemos visto distintos métodos de amortización que comparativamente para un mismo préstamo ofrecía distintas alternativas que obtenían el mismo resultado final: el reembolso total del capital y de los intereses pactados. El siguiente cuadro resume los distintos métodos vistos:
De nuevo, este último método podría adaptarse a incrementar la cuota cada período en lugar de hacerlo anualmente, como hemos mostrado en el ejemplo anterior.
Por otro lado, también es posible establecer un método de términos de amortización variables en progresión geométrica, cada año o cada período, sea respecto a la cuota o respecto a la amortización de capital. Para no extendernos en exceso, dejamos su desarrollo para otra ocasión.
Hasta aquí hemos visto distintos métodos de amortización que comparativamente para un mismo préstamo ofrecía distintas alternativas que obtenían el mismo resultado final: el reembolso total del capital y de los intereses pactados. El siguiente cuadro resume los distintos métodos vistos:
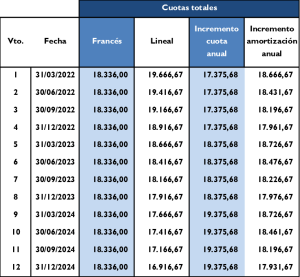
El cuadro representa una buena imagen de cómo, en función del método escogido, se puede adaptar el servicio de la deuda a las características particulares de cada prestatario, sin que ello suponga en absoluto comprometer el cobro por parte del prestatario de todas las cantidades pactadas.
Fuente: IDD Consultoría
